When to use the linear vs. rank correlation:
One of the useful statistical tools for finding the relationship between two or more variables is correlation coefficient. Depending on the type of data, different correlation coefficients can be used. Here, I am going to talk about linear and rank correlations. Before starting to look at linear and ranking correlations, let’s talk about different type of the data. In statistics, we have three types of data
- Numerical Data: This data is measurable, and four main operations can be performed on them. Numerical data can be broken down into discrete and continuous data. [1] 1. Discrete Data: Represents items that can be counted. Like the number of heads in 100-coin flips. 2. Continuous Data: Represent items that can be measured. Like temperature.
- Categorical Data: Represents characteristics; like gender.
- Ordinal Data: Represents the order; like movie ranking.
Linear correlation coefficient or Pearson Correlation Coefficient This correlation shows the relationship between two numerical variables. The Pearson correlation coefficient changes between -1 through 1. When Pearson correlation coefficient equals to one, it means that the two variables have a strong direct linear relation with each other. If it is -1, it shows that the two variables have strong invers linear relation. if it is 0, it shows that there is no linear relation between these two variables.
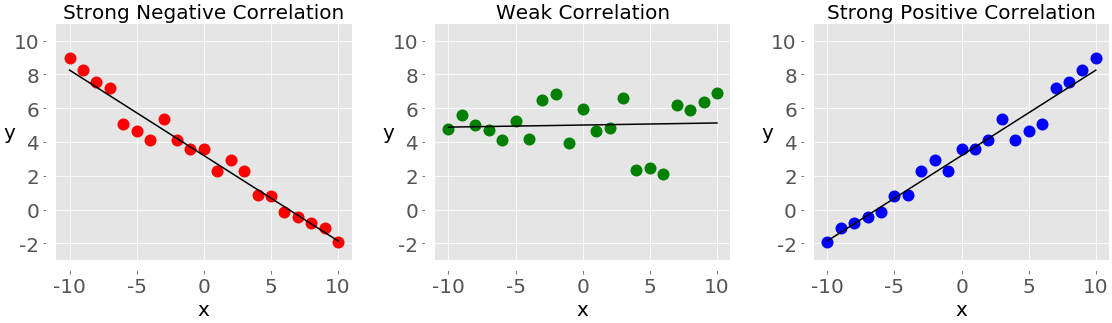
Ranking correlation or Spearman Correlation Coefficient
This correlation indicates the relationship between the two ordinal variables, in other words, the nonparametric corresponding to the Pearson correlation coefficient. If the orderings are similar, then the correlation is strong, positive, and high. However, if the orderings are close to reversed, then the correlation is strong, negative, and low. In other words, rank correlation is concerned only with the order of values, not with the particular values from the dataset. Similar to Pearson correlation, Spearman correlation coefficients are in the [-1,1] range. When both variables are monotonically increasing a function, the correlation coefficient would be 1, while when they are monotonically decreasing the function, the correlation coefficient would be -1. When the correlation is 0, they do no monotonically affect the function. [2]
SciPy Correlation Implementation:
>>Input:
import numpy as np
import scipy.stats
x = np.arange(0, 10)
y = np.array([2, 1, 4, 5, 8, 12, 18, 25, 13, 9])
Pearson = scipy.stats.pearsonr(x, y)
Pearson
>>Output:
(0.717608638601781, 0.019458339068724698)
>>Input:
Spearman = scipy.stats.spearmanr(x, y)
>>>Output:
SpearmanrResult(correlation=0.8303030303030302, pvalue=0.0029402270232795065)
Both functions’ outputs are touples and have two elements. The first one is correlation coeeficient and the second one is the p-value. P-value is astatistical method which is used in tetsting a hypothesis. You can also use dot notation for the Spearman.
>>Input:
scipy.stats.spearmanr(x, y).correlation
>>>Output:
1.0.8303030303030302
>>Input:
Spearman[0]
>>>Output:
1.0.8303030303030302
If you want to get the Pearson correlation coefficient and p-value at the same time, you can use the following code.
>>Input:
r, p = scipy.stats.pearsonr(x, y)
p
>>>Output:
>>p-value
0.019458339068724698
>>Input:
r
>>>Output:
>> Pearson correlation coefficien
0.717608638601781
Correlation in Pandas: For calculating statistics, Pandas is more convenient than SciPy. It offers statistical methods for both Series and DataFrames. For example, given two Series, with the same number of items, you can call .corr() on one of them with the other as the first argument:
>>Input:
import pands ass pd
x = pd.Series(range(0, 10))
y= pd.Series([2 ,1, 4, 5, 8, 12, 18, 9, 15, 13])
x.corr(y)
>>>Output:
0.8477537124567661
>>Input:
x.corr(y, method = 'spearman')
>>>Output:
0.8787878787878788
Sources:
[1] Types of Statistical Data: Numerical, Categorical, and Ordinal
[2] Linear Regression: SciPy Implementation